Law of physics:
Ohm’s law is stated as V=IR and it is fundamental to all electronics. Ohm’s law can be applied to a single component, to any group of components, or to a complete circuit. When the current flowing through any portion of a circuit is known, the voltage dropped across that portion of the circuit is obtained by multiplying the current times the resistance (Equation 2–1).
V=IR
In Figure 2–1, Ohm’s law is applied to the total circuit. The current, (I) flows through the total resistance (R), and the voltage (V) is dropped across R.
In Figure 2–2, Ohm’s law is applied to a single component. The current (IR) flows through the resistor (R) and the voltage (VR) is dropped across R. Notice, the same formula is used to calculate the voltage drop across R even though it is only a part of the circuit.
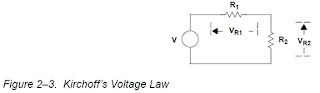
Kirchoff’s voltage law states that the sum of the voltage drops in a series circuit equals
the sum of the voltage sources. Otherwise, the source (or sources) voltage must be
dropped across the passive components. When taking sums keep in mind that the sum
is an algebraic quantity. Kirchoff’s voltage law is illustrated in Figure 2–3 and Equations
2–2 and 2–3.
Vsources =Vdrops.
V=Vr1+Vr2.
Kirchoff’s current law states: the sum of the currents entering a junction equals the sum
of the currents leaving a junction. It makes no difference if a current flows from a current source, through a component, or through a wire, because all currents are treated identically. Kirchoff’s current law is illustrated in Figure 2–4 and Equations 2–4 and 2–5.
Iin=Iout.
I1+I2=I3+I4.
Voltage Devider Rule:
When the output of a circuit is not loaded, the voltage divider rule can be used to calculate the circuit’s output voltage. Assume that the same current flows through all circuit elements (Figure 2–5). Equation 2–6 is written using Ohm’s law as V = I (R1 + R2). Equation –7 is written as Ohm’s law across the output resistor.
I =V / (R1+R2)
Vout= I R2
Vout=VR2 / (R1+R2)
A simple way to remember the voltage divider rule is that the output resistor is divided by
the total circuit resistance. This fraction is multiplied by the input voltage to obtain the out-put voltage. Remember that the voltage divider rule always assumes that the output resistor is not loaded; the equation is not valid when the output resistor is loaded by a parallel component. Fortunately, most circuits following a voltage divider are input circuits, and input circuits are usually high resistance circuits. When a fixed load is in parallel with the output resistor, the equivalent parallel value comprised of the output resistor and loading resistor can be used in the voltage divider calculations with no error. Many people ignore the load resistor if it is ten times greater than the output resistor value, but this calculation can lead to a 10% error.
Ohm’s law is stated as V=IR and it is fundamental to all electronics. Ohm’s law can be applied to a single component, to any group of components, or to a complete circuit. When the current flowing through any portion of a circuit is known, the voltage dropped across that portion of the circuit is obtained by multiplying the current times the resistance (Equation 2–1).
V=IR
In Figure 2–1, Ohm’s law is applied to the total circuit. The current, (I) flows through the total resistance (R), and the voltage (V) is dropped across R.
In Figure 2–2, Ohm’s law is applied to a single component. The current (IR) flows through the resistor (R) and the voltage (VR) is dropped across R. Notice, the same formula is used to calculate the voltage drop across R even though it is only a part of the circuit.
Kirchoff’s voltage law states that the sum of the voltage drops in a series circuit equals
the sum of the voltage sources. Otherwise, the source (or sources) voltage must be
dropped across the passive components. When taking sums keep in mind that the sum
is an algebraic quantity. Kirchoff’s voltage law is illustrated in Figure 2–3 and Equations
2–2 and 2–3.
Vsources =Vdrops.
V=Vr1+Vr2.
Kirchoff’s current law states: the sum of the currents entering a junction equals the sum
of the currents leaving a junction. It makes no difference if a current flows from a current source, through a component, or through a wire, because all currents are treated identically. Kirchoff’s current law is illustrated in Figure 2–4 and Equations 2–4 and 2–5.
Iin=Iout.
I1+I2=I3+I4.
Voltage Devider Rule:
When the output of a circuit is not loaded, the voltage divider rule can be used to calculate the circuit’s output voltage. Assume that the same current flows through all circuit elements (Figure 2–5). Equation 2–6 is written using Ohm’s law as V = I (R1 + R2). Equation –7 is written as Ohm’s law across the output resistor.
I =V / (R1+R2)
Vout= I R2
Vout=VR2 / (R1+R2)
A simple way to remember the voltage divider rule is that the output resistor is divided by
the total circuit resistance. This fraction is multiplied by the input voltage to obtain the out-put voltage. Remember that the voltage divider rule always assumes that the output resistor is not loaded; the equation is not valid when the output resistor is loaded by a parallel component. Fortunately, most circuits following a voltage divider are input circuits, and input circuits are usually high resistance circuits. When a fixed load is in parallel with the output resistor, the equivalent parallel value comprised of the output resistor and loading resistor can be used in the voltage divider calculations with no error. Many people ignore the load resistor if it is ten times greater than the output resistor value, but this calculation can lead to a 10% error.
CURRENT DIVIDER RULE:
When the output of a circuit is not loaded, the current divider rule can be used to calculate the current flow in the output branch circuit (R2). The currents I1 and I2 in Figure 2–6 are assumed to be flowing in the branch circuits. Equation 2–9 is written with the aid of Kirchoff’s current law. The circuit voltage is written in Equation 2–10 with the aid of Ohm’s law. Combining Equations 2–9 and 2–10 yields Equation 2–11.
Figure 2–6. Current Divider Rule
I=I1+I2
V=I1R1=I2R2
I=I1+I2=I2(R2/R1)+I2 =I2{(R1+R2)/R1}
Rearranging the terms in Equation 2–11 yields Equation 2–12.
I2=I(R1/(R1+R2)
The total circuit current divides into two parts, and the resistance (R1) divided by the total resistance determines how much current flows through R2. An easy method of remembering the current divider rule is to remember the voltage divider rule. Then modify the voltage divider rule such that the opposite resistor is divided by the total resistance, and the fraction is multiplied by the input current to get the branch current.





No comments:
Post a Comment